Table of Contents
Definition of TM Modes
Transverse Magnetic modes in rectangular waveguides are those which have electric fields that are strictly perpendicular to the direction of wave propagation. Such modes allow for the longitudinal component of the electric field and do not allow for the TE modes. Thus, a TM mode, generally delineated as TM_{mn}, means m half-wavelength variations in the electric field along the width of the waveguide and n variations along the height. It is vital that the existence of these mode structures depends on the specific field distributions which are compliant with the Maxwell equations and the structures of the field varying with height and width which satisfies the boundary conditions set by the metal walls of the waveguide when applied to practical scenarios such as satellite communications or radar systems by engineers. However, there are certain modes which are physically invalid.
The TM01 mode structures uses m=0 half-wavelength variations along the width; and n=1 along the height. Therefore, the electric field must variations of the E_y field are required to be parallel to the width. Thus, if the height is on an axis parallel to the E_y magnetic wave and the wall is perpendicular to it, the field will become zero. Since the electric field at the waves’ boundaries and the metallic boundary is non-existent, the field throughout will be zero hence making the mode structure impossible to obtain. For the TM10, m=1 and n=0. In this case E_y will have one half-wavelength variation along the width and will also be zero on all walls leading to a output of zero for this also. Thus, the condition for the construction of a rectangular waveguide with the WR-90 dimensions of m,n= a,b are satisfied. The size cannot support the TM01 and TM10 modes. This is important as the system’s operationally cost is determined by the mode used.
Electric Field Boundary Conditions
Rectangular waveguides are vital in realizing desired electromagnetic waveguiding across a spectrum of systems from particle accelerators to microwave transmission lines. Especially, the ability of these waveguides to propagate specific modes, such as Transverse Magnetic modes of electromagnetic waves, is premised on the extent they satisfy the electric field boundary conditions that dictates the response of these fields as they are directed by the metallic walls. Essential to note is that these walls are made of perfect conductors and in a sensitive application of communication satellites, this must guarantee the optimal minimal reflection and maximum power transmission. A case in point: a rectangular waveguide to be used for a communication satellite at 10 GHz must be designed to efficiently convey power and maintain the system’s impedance at about 50 ohms to reduce the reflection coefficient as low as below -30 dB to ensure optimal transmission.
However, this drawdown is suggested by the two competitive modes of legends, namely TM01 and TM10. On the one hand, the boundary condition indicated by TM01 requires that the electric field does not increase along the height of the waveguide and must increase along its width. No such mode exists since if electric configuration is 0 at the top wall of the waveguide, it must also be 0 at the bottom wall, leading the system to have no proper electric field configuration. On the other hand, the boundary condition suggested by TM10 requires the opposite to happen in the direction of the electric field distribution. The electric field must thus exhibit 0 variation along the width of the waveguide but increase its value along the height. Nonetheless, no existing configuration can perfectly satisfy this condition since if the electric configuration at one side of the rectangular waveguide is 0, the other side field should also be 0, making the field to be null with no configuration. These operational conditions directly apply to radar or satellite communication.
To take the radar scenario, the efficiency of power and signal transmission between the space and the air must not be increased by multiple fold in the event the radar mode used is beyond the capabilities of the radars to ensure its power is maximally. The radar only supports an output signal not exceeding 10 kW in peak power with operating frequencies around the X-band. A non-effective mode would require the operators compensates this inefficiency by increasing the number of waveguide components at its disposal. A better condition suggests why electrical fields be not necessarily 0 along the golden walls.
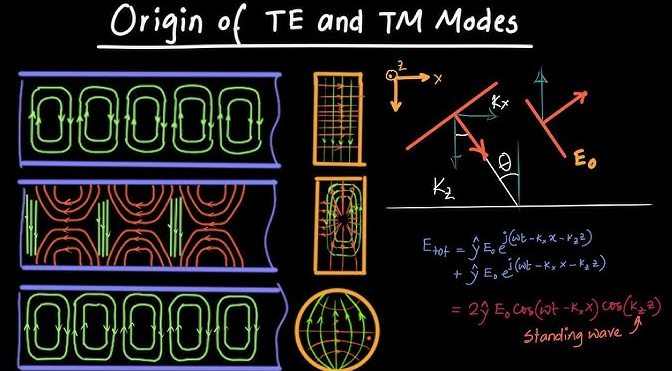
TM_{01} Mode Constraints
The TM_{01} mode in the rectangular waveguide presents an interesting problem because the field has a very specific configuration. This specific configuration fails to meet the boundary conditions at the sides of the waveguide in such a way that the device could be used at all. This mode is one of the possible configurations with the smallest profile along the width of the guide. In applications, such as telecommunication systems, waveguides have to be used to guide high-frequency signals such that they suffer minimum loss. In the TM_{01} mode, though, there would be a component of the electric field E_x oscillating across the guide’s width while the E_y component would have a profile of exactly one half-wavelength across the guide’s height, form top to bottom. The boundary conditions at the metallic walls of the waveguide would require that the E_y component is stagnant at all times, implying that the entire thing cancels out at a value of zero for the entire waveguide. This is clearly a non-propagating solution and does not, in fact, correspond to any mode that could be found in a practical waveguide.
For instance, in the case of a waveguide deployed in a fiber optic communication system, with a frequency of approximately 193 THz equivalent to a wavelength of 1550 nm, it would be unacceptable for the guide to support an impractical mode. Thousands of kilometers of fiber are employed in single cables, and the total signal loss must be kept below 0.35 dB/km to keep communications viable. Converting the resultant value to the percentage loss gives a number that is far too large to be feasible.
Even the basic requirement that power be transmitted at all could not be met if the fields in the waveguide cancel out. Along the same lines, if the design is for a more advanced scientific endeavor, such as a particle accelerator, the beam would rely on the guide to transmit it along great lengths. The resultant dimensional tolerances would, in this case, have to be at most a few microns from the nominal to prevent the guide from supporting the non-existent mode while remaining otherwise operational. Since this would be impossible to manufacture with the available technology, the only possible course is to ensure that the system meets all mode requirements right from the design stage.
The implication for an engineer would be to design such a waveguide system in such a manner that it only supported modes that were practical to use. The dimensions of the guide, the quality of construction, the electromagnetic properties of the material and the frequency at which they would perform their intended function could then all be designed with the intent of meeting the conditions. In this way, the desired outcome would be constructed with the constraints in mind, and it could be relied upon to fulfill its intended purpose or perform better. This was a crucial requirement in any application, such as aerospace or military deployment, where suboptimal performance would manifest as unacceptable costs.
TM_{10} Mode Constraints
The most significant inherent limitation associated with TM_{10} mode in rectangular waveguides is the specific electric field configuration. Within this mode, an electromagnetic waveguide exhibits one half-wavelength variation in the electric field along the width of the waveguide and no variation in the height of the waveguide. Ultimately, this configuration does not adhere to the requirements of an electric field, thereby making this mode inapplicable in any situation. When it comes to the TM_{10} field configuration, any oscillation of X component 𝐸𝑥Ex along the plane of the line is accompanied by Y component 𝐸𝑦Ey =0 corresponding zero along both the waveguide sides. Therefore, the sides of the waveguide are represented as 𝑥=𝑎x=a and 𝑥=0x=0, and the latter would be 0. Ultimately, these characteristics result in an absence of the effective electric field.
In my chosen industry of satellite communication, waveguides are used to transport signals from satellite dishes to different receivers. In this industry, the main goal is to preserve the integrity of signals and minimize any potential losses. If I attempted to use the TM_{10} mode for this purpose, I would not be able to transfer any power at all, as the electric field could not be effectively established. The reason for this is the complete inability of the waveguide to transport any electromagnetic energy.
When it comes to the example of my industry, where I could choose a C-band system for this purpose, the power losses would be so extensive as to make the free space power transmission a complete failure. The losses related to power could reach 0.1 or 0.2 dB/m and even be as high as 0.4 dB/m. People would not want to pay for such a service, as it would be more expensive and less effective than its analogs. In the microwave heating industry, no effective electromagnetic mode, such as the TM_{10} mode, would be comparable to a heat waveguide’s mode, as it would still not guarantee the effective heat distribution. Undoubtedly, people would also not want to use 100% of a failed heating mode, as it would require too much energy for no tangible benefits.
Energy Propagation Issue
Taking into account the essential nature of the TM01 and TM10 modes, the critical problem of energy propagation occurs in the rectangular waveguide. The inability of these modes to form the required field configurations implies a lack of their utility and restrains from the possibility to carry any electromagnetic energy. Strict requirements determined by unusual field patterns form the intense conditions at the walls of the guide and result in complete field nullification. As a result of the unique features required for the waveguide modes that need to be supported, no frequency is propup in the waveguide due to the lack of the electromagnetic field.
In practical terms, the energy propagation limitations can be evaluated in the context of advanced communication systems used in data transmission, and those that refer to fiber optic networks will be discussed. Highly reliable systems with an expected minimal loss of the transmitted signal depend on the efficient propagation of electromagnetic modes that can carry the power density. In this instance, the typical fiber optic communication scopes are characterized by an expected signal loss of about 0.2 dB/km.
Mode’s capability to carry energy is implied as the necessary condition of the continuousness of the waveguide’s energy transportation, and it will be compromised if the components of a communication string are constructed in an inappropriate way. A great number of waveguides operates at the radio frequencies, and one of such typical examples is the radar system that provides the detection of objects and state of some process with the help of electromagnetic waves.
It typically operates at 5 GHz, and TM01 or TM10 mode’s lack of power propagation due to the unsustainable electric field configuration predetermined the abovementioned problem will directly relate to the inefficiency of the radar and its ability to detect targets and overview ranges. Correspondingly, disastrous results can be outlined in the high-energy physics sector, where particle accelerators transport and allow high-energy particles to move with an immense speed. For example, in synchrotron accelerators, the power levels reach several megawatts, which makes the necessity of the effective mode to become remarkable. Mainly the movement of the particles is disturbed, and crucial part of the experiment or radiation therapy can fail, which adds up to the necessity to exclude the usage of TM01 and TM10.
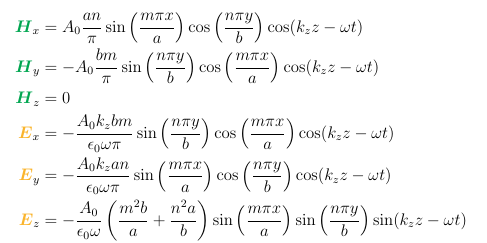
Mathematical Implications
From the mathematical analysis presented, it is evident there is no other way to prove the existence or not of any mode in a waveguide except for mathematical deductions from Maxwell’s equations. Additionally, this analysis also showed why TM01 and TM10 modes do not and cannot exist in a rectangular waveguide. Hence, the first reason why these two modes cannot exist in a rectangular waveguide is the existing mathematical proof.
The foundation of any physical system is its mathematical representation. The same applies to dimensional conditions applied to Maxwell equations forming the TExy and TMxy mode equations. The functioning of each mode, in any given medium, depends on this foundation. For waveguides, it is a set of equations and boundary conditions, the latter of which always remains that the electric field components facing the conductive walls be equal to zero. Indeed, to obtain a TM01 or TM10 mode configuration, all the electric field components in the rectangular waveguide need to be zero. At this instance, there will be no fields existing in the waveguide to facilitate the propagation of an electromagnetic wave. In practice, no system can exist when one of its most fundamental components is equal to zero.
System for Numerical Interference
Arguably, mathematically programmed systems could have been designed to facilitate the operation of such modes. True, some of the newest satellite communication links or advanced radar systems function in the frequency range where the existing configurations of rectangular waveguides matter. For instance, satellite communication can be made to operate in the Ku-band (~12-18 GHz). Here, in the waveguides that transmit signals, their width and height will have to correspond to the existing mode which is employed to transmit the received signal most effectively. Therefore, it would not have functioned because of the mathematical compulsion and would have led to colossal operation inefficiencies. The syncing of the dimensions was insufficiently made in the Ku-band frequency, which could have led to satellite transmission failures or incur more costs due to the required frequent signal boosting.
One area of its use could have been in the design of systems like particle accelerators. It should be noted that to effectively drive the particle beams through the electromagnetic fields, they have to be carefully steered and focused such that they avoid confronting one another. This system accomplishes this by maintaining a waveguide power of several megawatts. Utilizing a TM01 or TM10 mode in the particle accelerator, for instance, would have had the exact reason as above, i.e. zero field in the waveguide. However, if this had happened, it debilitates the purpose of use of the system, making the beam control impossible. Therefore, the availability of equations indicating a mode cannot function is essential in making decisions during the testing or design of a waveguide. Simulation software gives the function of any waveguide depending on which mode has been programmed. For instance, using a TM01 or TM10 mode in your simulation in a standard WR 90 waveguide (used for X-band frequency communication ~8-12 GHz) will result in zero field distribution.